Understanding Projections, “True Talent Level”, and Variability

This is the second in a series of posts about projections. The first part was about the methodology behind each projection system. In this section, we look at what projections are actually telling us.

If you’re new to projections and want to use them to, say, help with your fantasy team, it’s easy to make a common mistake: underestimating the built-in variability in projections. Many people – and I used to be among this group myself – view projections as hard and fast guesses at a player’s production this next season. Most people get into projections as a result of fantasy baseball, so this makes sense; we all want to know which player is going to hit 30 homeruns this next season and which will steal 40 bases. However, projections are actually measuring something different than a player’s expected production: they’re measuring a player’s true talent level.

This might seem like an arbitrary distinction, but trust me, it’s not. As we all know from our day-to-day lives, having a “true talent level” at a particular skill does not necessarily mean you’ll perform at that level every single time in the future. Our minds love to ignore variability and instead treat outcomes as solely talent-driven, but the world doesn’t work that way. Let’s consider a couple examples.

Let’s start with something simple: flipping a coin. We’d expect that a normal coin would have a “true talent level” of landing heads 50% of the time, right? If you flipped that coin 100 times, though, it may be that you’d end up with 53 heads and 47 tails….or with 45 heads and 55 tails. You’d be most likely to end up with a result close to 50/50, but it’s no guarantee that things would end up precisely at the coin’s true talent level every single time.

If that’s not convincing enough (after all, there’s no “talent” involved in whether a coin comes up heads or not), consider basketball. Each of us has a specific true talent level for hitting free throws, some better than others. I’m horrible at basketball, so I’d place myself around a 30% talent level, meaning I’m likely to make around three baskets out of every ten. If I went out and shot five different sets of 10 free throws, though, I wouldn’t necessarily make three every single time; my scores may look something like 2, 4, 5, 3, 1. This variability doesn’t mean my true-talent level is wrong: it just means that there’s no guarantee we’ll perform exactly at our true talent level every time we perform. Sometimes we may over-perform, while others we may under-perform.

You’ll sometimes hear people refer to projections as “50th percentile projections”, which expresses exactly this concept: 50% of the time a player will over-perform their projection, while 50% of the time they’ll under-perform it. Players and teams are most likely to perform at a level close to their projection level, but that’s no guarantee. Variability for teams and players typically follows the normal distribution:

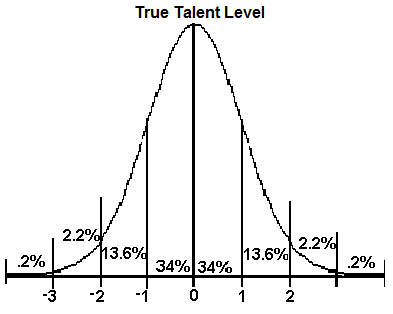
This is the statistical way of showing how likely a person (or team) is to perform close to their true talent level. Say we simulate this upcoming season 1,000 times with the Red Sox as a 94-win true talent level team. According to this graph, we’d expect the Sox to finish 68% of those seasons within one standard deviation of 94 wins, and 95% of them to fall within two standard deviations. “Standard deviation” simply refers to the predicted amount of variability with a team or player, with major league teams typically having a standard deviation of six games over a 162-game season.*

*Someone smarter than me, feel free to disagree and disprove this – that isn’t my calculation, so I’m not wed to it. I’d argue that standard deviation varies on a team-by-team basis, with some teams having a slightly tighter deviation and some having a slightly wider one, but as an average six games seems to make sense.

In other words, say we project David Wright to hit 20 homeruns this season. That projection isn’t saying that he’s going to hit exactly 20 homeruns, but instead that he’s 68% likely to hit within one standard deviation of 20 homeruns. With that in mind, Wright hitting either 15 or 25 homeruns wouldn’t necessarily prove the initial projection “wrong”: it just means that Wright’s season varied from his projection, and we can use that information to better project his true-talent level going forward.

How do we measure that variability? What’s the typical standard deviation for homeruns, batting average, wOBA, etc? Those questions I don’t have a specific answer to, as there are many conflicting issues in play. For one, projections are only best guesses at a player’s true talent level, and there are many things we can’t know or measure: the exact effect of injuries, exactly how a specific player will age, the exact amount of talent residing in a player. We can make good guesses based on historical trends and what we see on a day-to-day level, but “true talent level” is an ethereal concept and can’t be measured like you can a temperature. As such, projections will never be perfect.

Also, the standard deviation for specific statistics can be different depending on the player. Adam Dunn has almost exactly 40 homeruns for six seasons in a row, but there are also players like Jose Bautista and Ben Zobrist that have had wildly varying power numbers over the past few seasons. Each aspect of each projection therefore has a different level of confidence to it, and you have to be able to assess that confidence by looking through a player’s career and determining if you think that projection has a wide or tight standard deviation.

So the next time you start looking through projections, remember to take variability into account. Our minds love to eschew probability and uncertainty – why do you think casinos make such a killing? – but understanding this concept can keep you from drawing faulty conclusions from projections. Embrace uncertainty, and it might help you beat the house (or beat your friends at Fantasy).